Introduction to Robotics-Stanford 笔记 LEC4

LEC4 Manipulator Kinematics 机械臂运动学

正运动学是一种随动坐标系与基坐标系之间的关系

Link Description 连杆描述

1

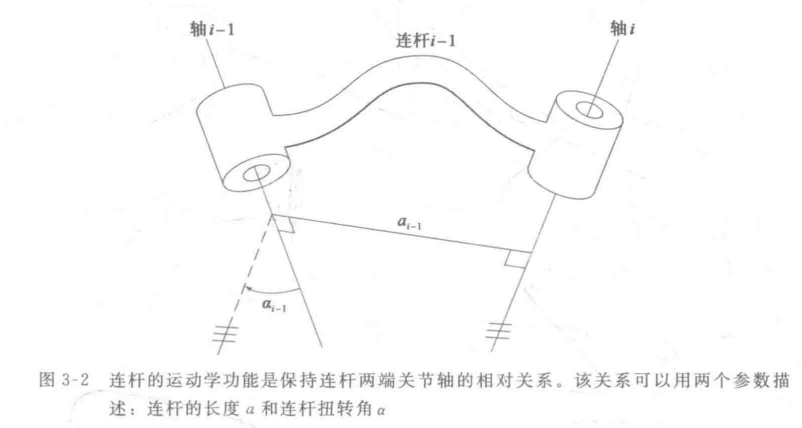
对于一个连杆，其两端有两个关节轴，如何描述这两个轴的关系？为了去确定机械臂两个相邻关节轴的位置关系，可把连杆看作一个刚体。用空间中的直线来表示关节轴。显然，在描述连杆的运动时，一个连杆运动可用两个参数描述，这两个参数定义了空间中两个关节轴之间的相对位置（距离和夹角）

• ：Link Length 连杆长度
  • mutual perpendicular 两轴之间公垂线的长度
  • unique except for parallel axis 是唯一的（平行轴例外）
  • 是常数
• ：Link Twist 连杆扭转角
  • measured in the right-hand sense about 假设一与公垂线垂直的平面，将轴和轴投影到平面上，用右手定则从轴绕到轴测量两轴线之间的夹角
  • 是常数

一种特殊情况是Intersecting Joint Axes（两个关节轴相交），在这种情况下，考虑轴和轴形成的平面，并且做出该平面的垂线，就会得到两个轴的公垂线向量。注意的方向会影响的方向。一般可以让指向末端执行器。

Link Connection 连杆连接的描述

image.png

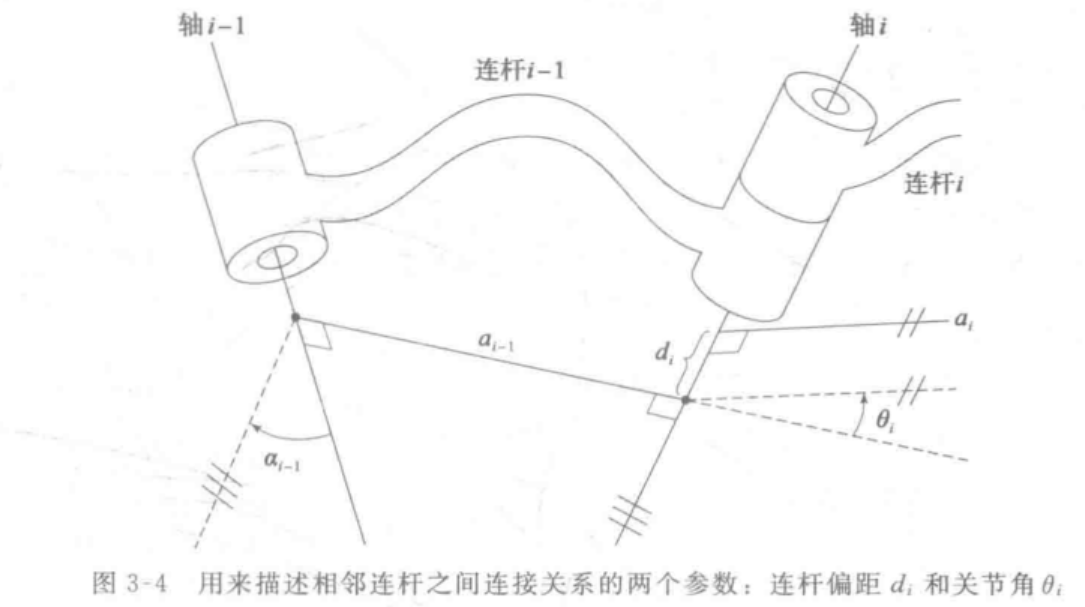
描述连杆连接时，同样只需要两个参数，这两个参数完全确定了所有连杆是怎么连接的。

处于运动链中间位置的连杆

• ：Link Offset 连杆偏距
  • variable if joint is prismatic
  • 对于转动关节来说是固定不变的，但对于平移关节，就会沿着移动方向影响后续连杆的运动。如果是平移关节，那么是变量。
• ：Joint Angle 关节角
  • variable if joint is revolute
  • 对于一个转动关节，是变量

和之间总有一个是常数，另一个是变量。（取决于关节类型）

运动链中首端和末端连杆

首先是连杆长度和连杆扭转角。连杆长度和连杆扭转角取决于关节轴线和，因此轴1到n确定了和。对于首端和末端连杆，其参数习惯设定为和，相当于把轴0和轴1放在同一个坐标轴上重合，这样可以减少正运动学中使用的参数量。

其次是连杆偏距和关节角。注意，和取决于连杆i-1和i，这意味着我们实质上是定义和。如果关节1为转动关节，则的零位可以任意选取，并且设定。同样，如果关节1为移动关节，则的零位可以任意选取，并且设定。

以上方法也适用于关节n。

连杆参数 Denavit-Hartenberg Parameters

由上可知，机器人的每个连杆都可以用4个运动学参数来描述，其中两个参数用于描述连杆本身()，另两个参数用于描述连杆之间的连接关系()。通常，对于转动关节，为关节变量，其他三个连杆参数是固定不变的；对于移动关节，为关节变量，其他三个连杆参数是固定不变的。这种用连杆参数描述机构运动关系的规则称为Denavit-Hartenberg方法，即

例如，对于一个6关节机器人，需要用18个参数就可以完全描述这些固定的运动学参数。如果是6个转动关节的机器人，这时18个固定参数可以分为6组表示。

连杆坐标系的定义

为了描述每个连杆与相邻连杆之间的相对位置关系，需要在每个连杆上定义一个固连坐标系。根据固连坐标系所在连杆的编号对固连坐标系命名，因此，固连在连杆上的固连坐标系称为坐标系。

运动链中间位置连杆坐标系的定义

通常按照如下方法确定连杆上的固连坐标系：坐标系的轴称为，并于关节轴重合，坐标系的原点位于公垂线与关节轴的交点处。沿方向由关节指向关节。

当时（相交轴），垂直于和所在的平面。按右手定则绕轴的转角定义为，由于轴的方向可以由两种选择，因此的符号也有两种选择。轴由右手定则确定，从而完成了对坐标系的定义。

image.png

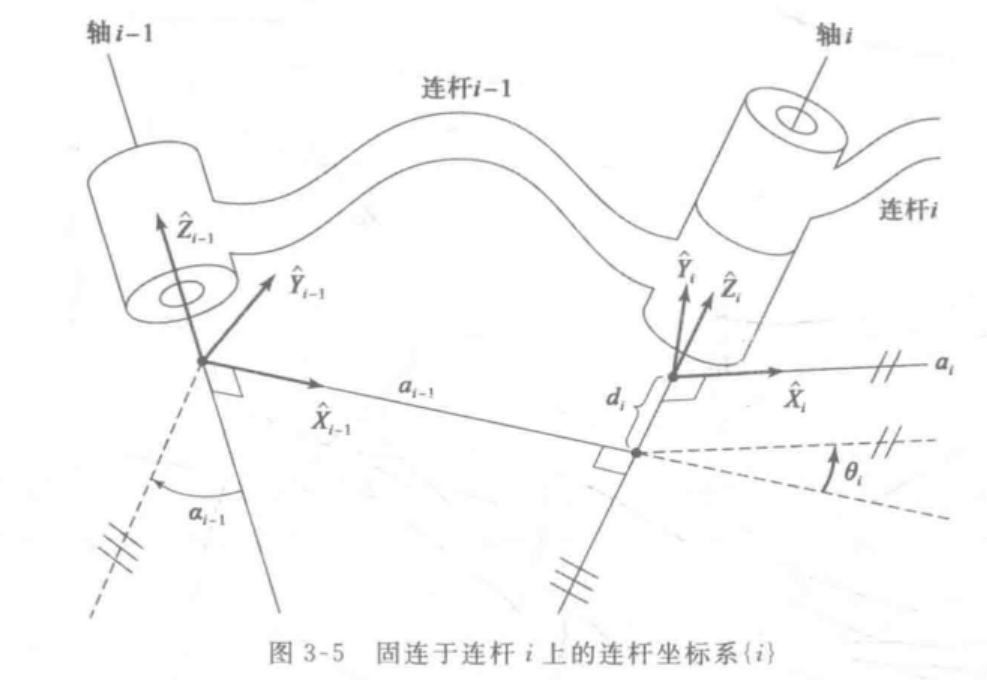
运动链中首端连杆和末端连杆坐标系的定义

固连于基座（即连杆0）上的坐标系为坐标系。这个坐标系是一个固定不动的坐标系。

参考坐标系可以任意设定，但是为了使问题简化，通常设定轴沿关节轴1的方向，并且当关节变量1为0时，设定参考坐标系与坐标系重合。

• 首端连杆
  • 当关节1为转动关节时，，当时，
  • 当关节1为移动关节时，，当时，
• 末端连杆
  • 当关节n为转动关节时，，当时，
  • 当关节n为移动关节时，，当时，

总结一下四个参数：

• : distance along
• : angle about
• : distance along
• : angle about

例子：

image.png

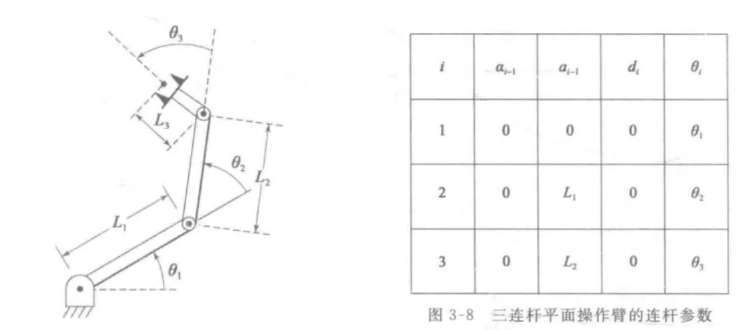
机械臂运动学 Forward Kinematics

连杆变换的推导

描述连杆的四个参数分别对应一个简单的坐标系变换，一共四个坐标系变换。

我们希望建立坐标系相对于坐标系的变换。一般这个变换是由4个连杆参数构成的函数。对任意给定的机器人，这个变换是只有一个变量的函数，另外3个参数由机械系统确定。通过对每个连杆逐一建立坐标系，我们把运动学问题分解为n个子问题。为解决每个子问题，即，我们将每个子问题再分解为4个次子问题。4个变换中的每一个变换都是仅有一个连杆参数的函数。为每个连杆定义3个中间坐标系——。

image.png

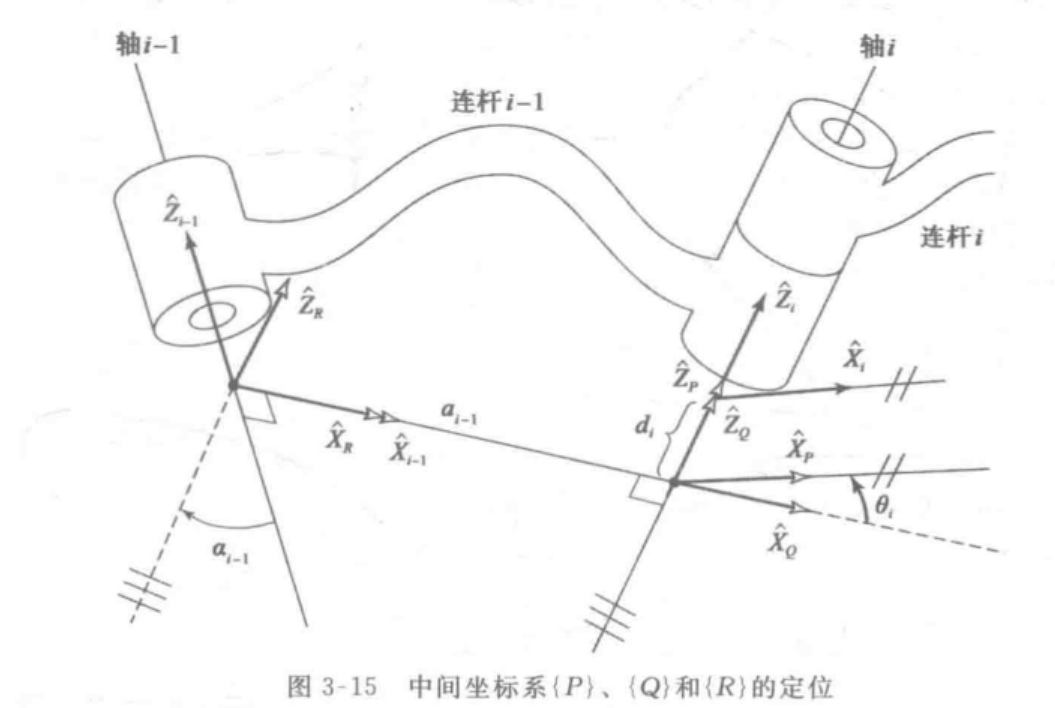
由于旋转 ，因此坐标系 与坐标系 不同；由于位移 ，因此坐标系 与坐标系 不同；由于位移 ，因此坐标系 与坐标系 不同；由于转角 ，因此坐标系 与坐标系 不同；由于位移 ，因此坐标系 与坐标系 不同。

整个过程可以写成

考虑每一个变换矩阵，上式可以写成

计算可得

结合上面例子中给出的参数表，就可以写出整个变换矩阵

连杆变换的连乘

如果已经定义了连杆坐标系和相应的连杆参数，就能直接建立运动学方程。由连杆参数值，我们可以计算出各个连杆变换矩阵。把这些连杆变换矩阵连乘就能得到一个坐标系相对于坐标系的变换矩阵

变换矩阵是关于个关节变量的函数。如果能得到机器人关节位置传感器的值，机器 人末端连杆在笛卡儿坐标系里的位置和姿态就能通过计算出来。