DDPM(Denoising Diffusion Probabilistic Models)论文阅读笔记

论文：Denoising Diffusion Probabilistic Models

前言

最近在研究Diffusion Policy，跟DDPM关系非常密切，于是读了下DDPM的文章，写篇笔记，顺便挖个坑，记录一些生成模型的研究。DDPM（以下简称扩散模型）不仅在图像生成方面有着非常广泛的应用，而且现在在机器人学习也有研究前景。在读了扩散模型的论文和一些解读的博客后，发掘其中有许多细节需要仔细探讨。（实际还有很多细节还没理解🤡）

什么是Diffusion Model（扩散模型）？

首先需要理清一点，借用生成扩散模型漫谈（一）：DDPM = 拆楼 + 建楼一文所述，传统的扩散模型实际上是一类模型，涉及到能量模型（Energy-based Models）、得分匹配（Score Matching）、朗之万方程（Langevin Equations）等等，DDPM也用了“扩散模型”这一名称，但实际上除了采样过程的形式有一定相似处外，DDPM与传统基于朗之万方程采样的扩散模型可以说完全不一样，传统的扩散模型的能量模型、得分匹配、朗之万方程等概念，其实跟DDPM及其后续变体都没什么关系。

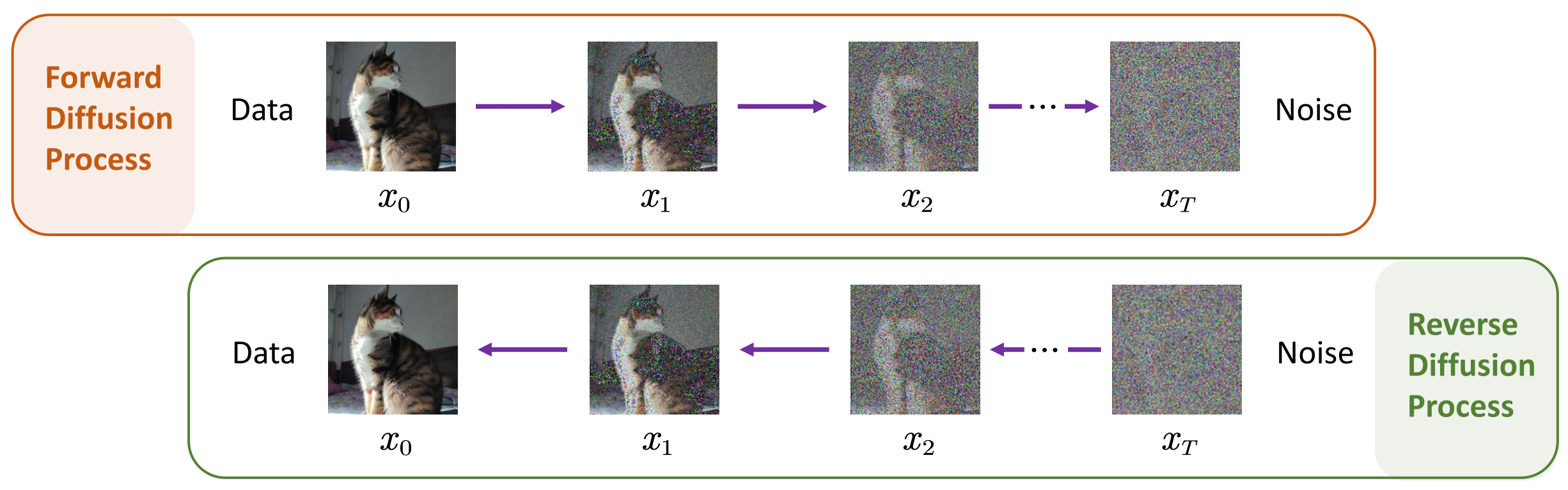
扩散模型的核心是两个过程/概念：前向过程（加噪过程、扩散过程）和反向过程（去噪过程）。直白理解，前向过程就是逐步地往一张完好的图像里添加噪声，让其逐渐靠近高斯噪声，整个过程可以表示为：

现在在前向过程中，我们知道每一步加噪的过程，即，如果我们能通过某种方式找到其对应的反向过程，即，将这种变换关系记作，反复地执行 $、$ ，是不是就能逐步地从还原回原始的图像？

以上就是扩散模型最核心的思想。

这里首先要补充一个重要特性：

重参数（Reparameterization）

重参数技巧在很多工作中有所引用。如果我们要从某个分布中随机采样 (高斯分布) 一个样本，这个过程是无法反传梯度的。而这个通过高斯噪声采样得到的过程在 diffusion 中到处都是，因此我们需要通过重参数技巧来使得他可微。

最通常的做法是把随机性通过一个独立的随机变量 (ϵ) 引导过去。即如果要从高斯分布采样一个，我们可以写成：

上式的依旧是有随机性的，且满足均值为，方差为的高斯分布。这里的，可以是由参数的神经网络推断得到的。整个采样过程依旧梯度可导，随机性被转嫁到了上。

前向过程（Forward Diffusion Process）

首先声明几个符号的关系：令

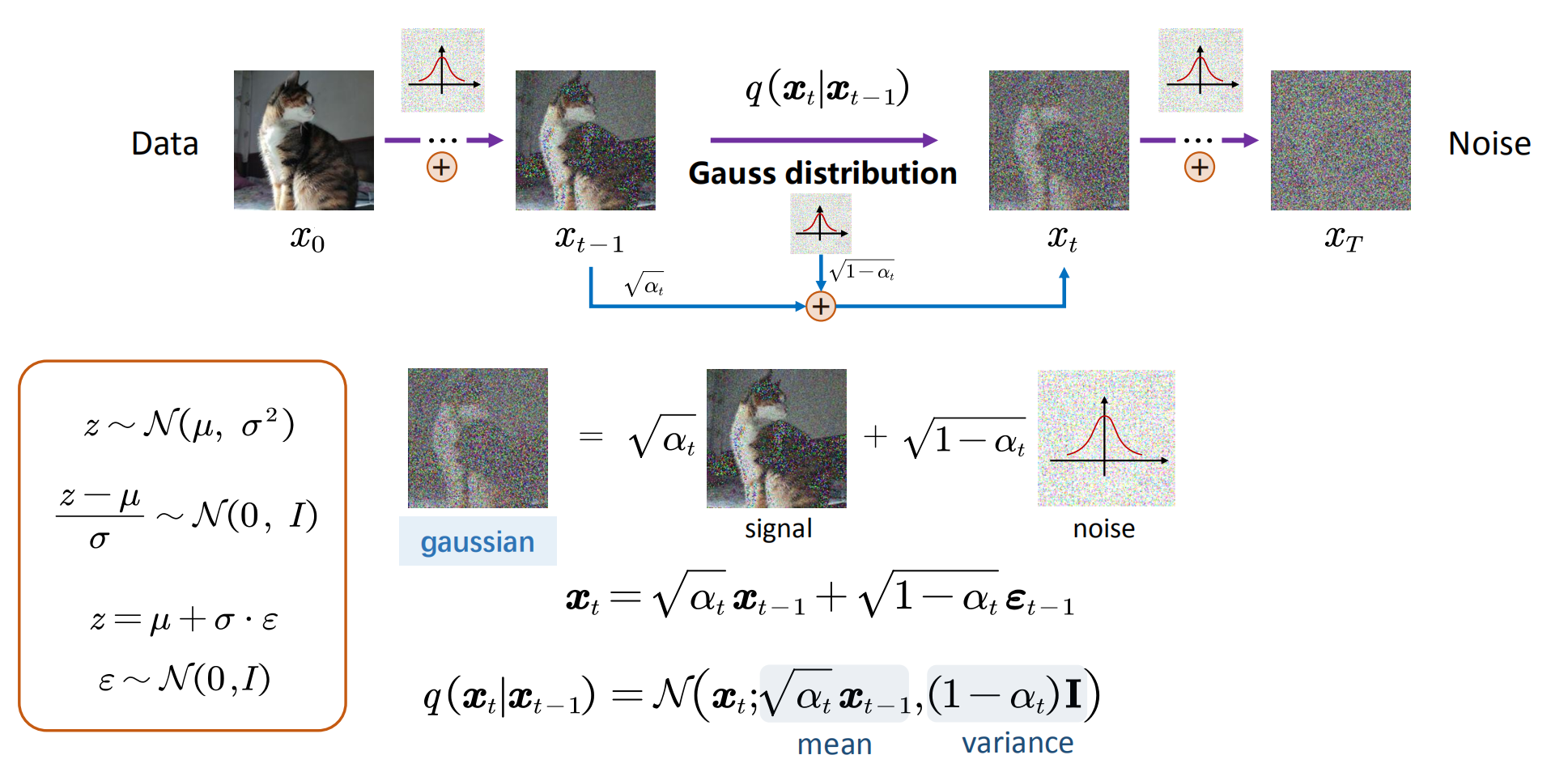
DDPM将前向过程建模为

这个公式就是一步步给图像添加噪声的公式。

通常很接近0，可以理解为加噪过程中对原图像的损坏程度，噪声的引入代表着对原始信号的一种破坏，引用论文的原话：

The forward process variances can be learned by reparameterization or held constant as hyperparameters, and expressiveness of the reverse process is ensured in part by the choice of Gaussian conditionals in ， because both processes have the same functional form when are small. 正向过程方差可以通过重新参数化来学习，或者作为超参数保持不变，而逆过程的表达能力部分由中高斯条件的选择来保证，因为当很小时，两个过程具有相同的函数形式。 这里的后面会讲到

这个前向过程也可以用

来表示，也被称为“近似后验”（approximate posterior），整个前向过程符合马尔可夫性质，是一个马尔科夫链。

图示：

反复执行加噪步骤，我们可以推导：

这是前向过程中的关键性质。也可以表示为：

这被称为Close form。

从这个形式，我们可以得出两个结论：

任意时刻的可以由和表示，这就为计算提供了极大的便利。
通过选择合适的（论文里是人为设置），当时间步时，，实际上会被转换为高斯噪声。

以上就是前向过程，不涉及到训练。

反向过程（Reverse Diffusion Process）

如果把前向过程视作“加噪”过程，那么反向过程就是“去噪”过程，即的过程。

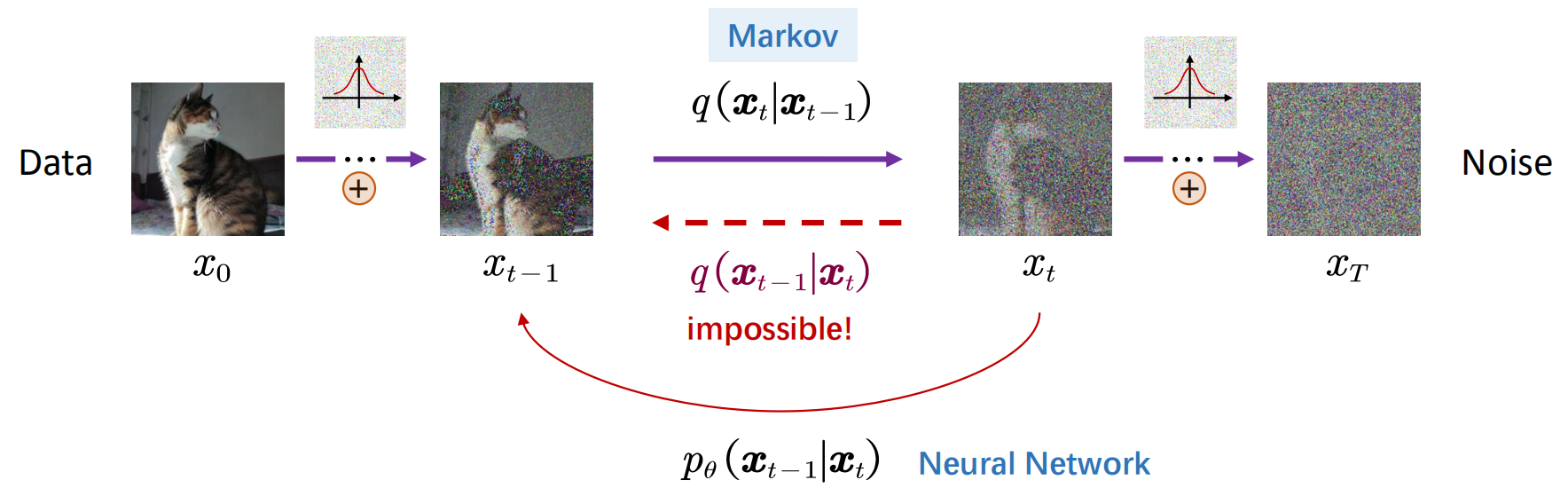
在前向过程中，是已知的，如果能求解目标分布，这个问题救迎刃而解了。然而，我们无法简单推断。因此换个思路，我们知道神经网络是通用函数近似器，可以利用神经网络去预测一个反向的过程，但是要怎么预测、怎么训练？这是反向过程的核心问题。

已经有文献证明，如果满足高斯分布且足够小，仍然是一个高斯分布。因此我们可以假定也是一个高斯分布：

前面说到，反向过程是训练一个网络去预测，但是我们无法直接得到，那么该怎么训练？这里引入了一个很巧妙的方法，那就是我们不去找，而是找，把条件分布变成联合分布。由于前向过程符合马尔可夫性质，所以这两个东西实际是等价的，但是后者是可以通过贝叶斯公式推导得到的，推导过程如下：

至此，将反向过程全部变回了正向过程，而正向过程我们是知道的，这里的每一项都可以求。

这里有一个容易绕晕的点（我自己一开始也绕晕了），既然反向过程都已经表示出来了，为什么不能直接用呢？因为这里讨论的是训练过程，我们是知道的，而推理时是不知道的。

式（7）中的各项也都是符合高斯分布的，如下：

因此，式（7）可以继续往下推导（推导过程省略了，可以通过高斯分布的表达式推，直接给出结果）：

在这里，我们令，。

由于可以是训练时人为设置的一组超参数，所以这里可以视为一个常数。因此，训练的关键其实落在了如何预测。

由Close-Form可以求出：

将式（8）代入式（7）中，可以将化简为：

这个式子中，也只有是未知的，因此，我们实际上是需要神经网络去预测一个“噪声”。

在训练好网络后，我们就可以通过前文提到的重参数从去一步步采样得到：

为了进行随机采样，这里的最后有一个高斯项。

以上就是反向过程，核心就是设计一个神经网络去预测分布的均值，而预测均值实际上是通过预测噪声实现的。

总结反向过程：

每个时间步通过和来预测高斯噪声，随后根据式（9）得到均值
得到方差，在DDPM中使用untrained，且认为和结果近似
根据式（5）得到，利用重参数得到

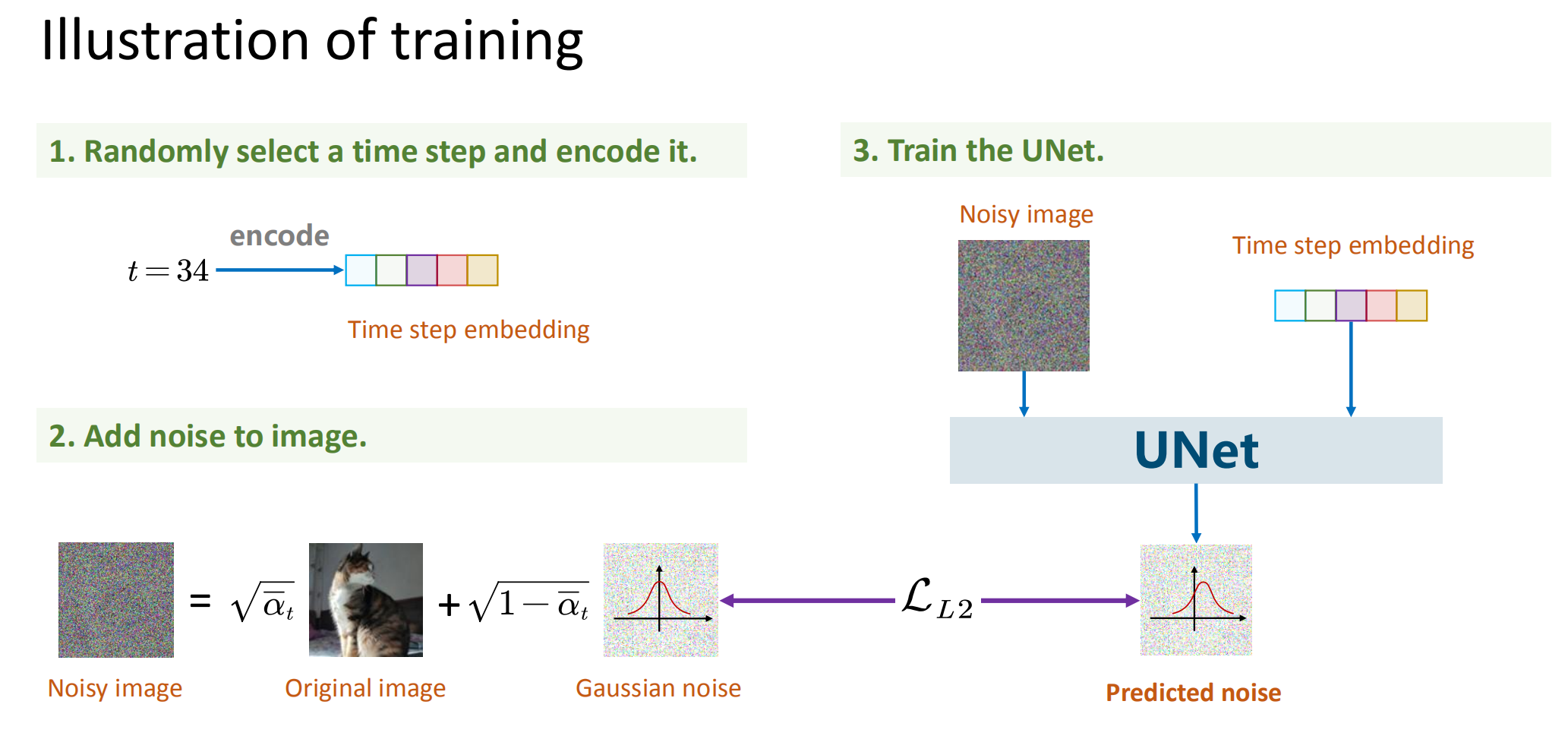
训练过程

优化目标——最大似然估计

这里其实我没看懂，简单记录一些式子，等以后看懂了继续补充。

论文原话：Training is performed by optimizing the usual variational bound on negative log likelihood.

下面分析一下。实际上这是在优化下的交叉熵：

可以使用变分下界（VLB）来优化负对数似然。由于KL散度非负，可得到：

$与无关$

这就是ELBO（证据下界/变分下界）。对左右取期望，利用重积分中的Fubini定理，可以得到：

$定理$

能够最小化即可最小化我们的目标损失(11)。

进一步对推导，可以得到熵与多个KL散度的累加，具体可见文献【】中的推导。这里直接给出结果：

由于前向q没有可学习的参数，而则是纯高斯噪声，可以当作常量忽略。而则可以看作拉近2个高斯分布

和，根据多元高斯分布的KL散度求解：

DDPM在训练时使用的是以下变体：

总结训练过程：

获取输入，从随机采样一个t
从标准高斯分布采样一个噪声
最小化

重要公式总结

forward（close-form）：
optimization：
reverse：
training：
sampling：

DDPM论文提供的训练/测试（采样）伪代码：

其他细节

降低方差

原则上来说，优化损失函数（17）就可以完成DDPM的训练，但它在实践中可能有方差过大的风险，从而导致收敛过慢等问题。式（17）中实际包含了4个需要采样的随机变量：

从所有训练样本中次采样一个
从正态分布中采样和（两个不同的采样结果）
从中采样一个

要采样的随机变量越多，就越难对损失函数做准确的估计，反过来说就是每次对损失函数进行估计的波动（方差）太大了。实际上我们可以通过几个积分技巧将和合并成单个正态随机变量，从而缓解方差过大的问题。这一点就不详细记录了，因为我没看懂🥲

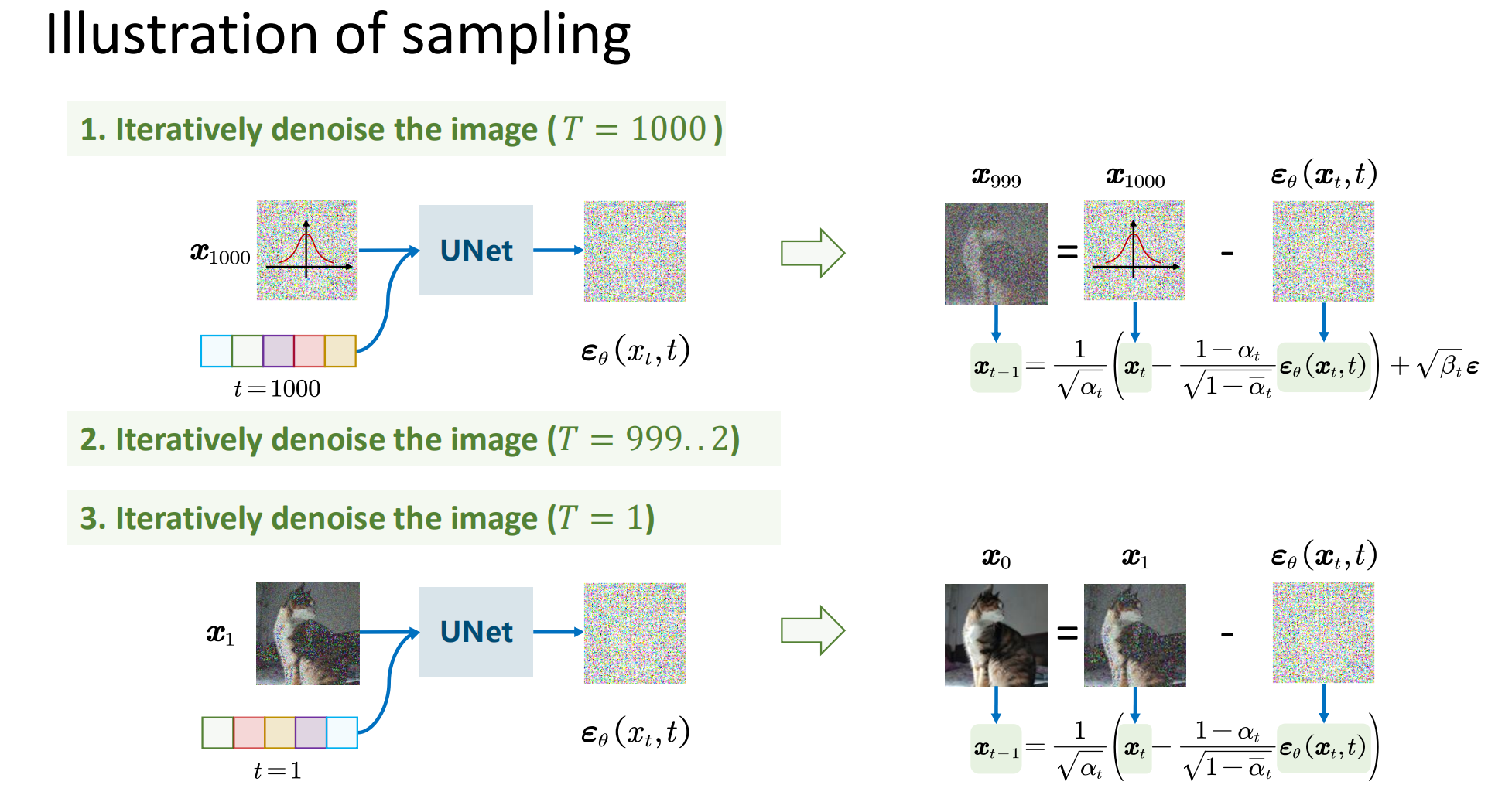
递归生成（采样）

训练完之后，我们就可以从一个随机噪声出发执行步采样公式（10）来进行生成。

一般来说，我们可以让，即正向和反向的方差保持同步。这个采样过程跟传统的扩散模型的朗之万采样不一样的地方在于：DDPM的采样每次都从一个随机噪声书法，需要重复迭代步来得到一个样本输出；朗之万采样是从任意一个点出发，反符迭代无限步，理论上这个迭代无限步的过程中，就把所有数据样本都生成过了。所以两者除了形式相似之外，实质上是两个截然不同过的模型。