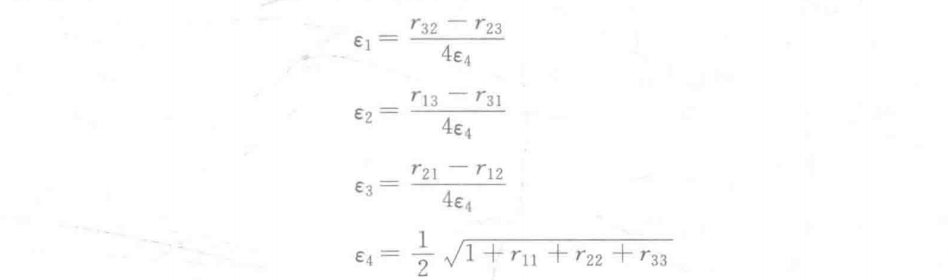Introduction to Robotics-Stanford 笔记 LEC3

没怎么听懂的一节，还得慢慢啃🤯

Homogeneous Transform Interpretations

Description of frame

描述B相对于A的坐标系变换

Transform mapping

将坐标系B中的点P的描述映射到坐标系A中(点不变，向量变)

Transform operator

将坐标系A中的向量变换成向量(坐标系不变)

Transform Equation

Compound Transformations 复合变换

引入第三个坐标系C，假设有一个从C到B的变换和一个从B到A的变换，要研究从C到A的变换

假设C中有一个向量：

• 左上角保持相对于旋转的结构，有相同的旋转属性
• 右上角可以看作是将C的原点相对于B的向量映射到A中

Transform Equation

假设有A, B, C, D四个坐标系，A→B→C→D→A这样的复合变换，构成一个闭环的变换组，最终的总变换矩阵是一个单位阵，即

假设这四个变换其中有一个是未知的，就可以通过以上恒等式求解出来，例如：

Representations

我们所关心的问题在于末端执行器，末端执行器实际是整个操纵问题的目的，即我们关心如何在空间中定位这个末端执行器，以及如何将其移动到某个位置

假设从Base frame基坐标系到末端执行器坐标系的齐次变换是，当完成正向运动学时，末端执行器相对于基坐标系的变换由给出，并且这个来自整个操纵器的描述，包括连杆长度、倾斜角度、连杆特性等，并且它是关节角度的函数（核心），即会随着关节角度变化而变化，机器人配置（configuration）会影响末端执行器位置。所以我们要找到这个4x4矩阵T作为关节角度的函数，这个矩阵将包含每个配置的齐次变换的描述。

所以我们需要做的是从T中提取位置和方向的描述

End-Effector Configuration Parameters

其中代表位置（x,y,z），代表方向。回忆一下齐次变换矩阵，可以发现

• 的信息在T的最后一列的前三个元素构成的向量里
• 的信息在T左上角的3x3子矩阵里，即旋转矩阵

Position Representations 位置表示

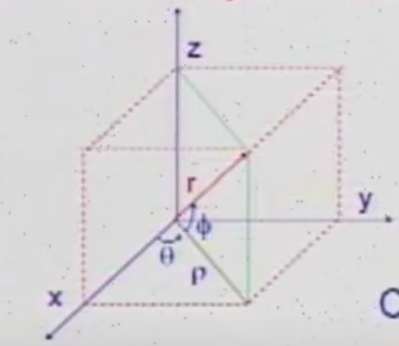
• Cartesian 笛卡尔坐标：
• Cylindrical 圆柱坐标：
• Spherical 球坐标：

大多数情况下可以使用笛卡尔坐标；如果希望操纵工具沿轴平移进行灵巧操作，可能会使用圆柱坐标。对于不同的任务，使用不同的位置表示可能会更有优势。

Rotation Representations 旋转表示

Rotation Matrix 旋转矩阵

• 包含旋转中的所有信息的表示

从齐次变换T中可以提取这个旋转矩阵。回忆一下旋转矩阵，实际是X, Y, Z在基座标系中的分量，现在我们可以用它构建一个表示

Direction Cosines 方向余弦

上面两种表示都需要9个参数，而表示方向的自由度实际上只有3个，我们可以考虑以下这些向量之间的约束

Constrains 约束

都是模长为1的单位向量，且之间两两正交，这里一共有3+3=6个约束

因此9个参数-6个约束=3个自由度

实际上旋转矩阵的方向余弦都是冗余表示，即参数并不是独立的，这会产生一个问题。 假设要让机器人做一个移动物品的简单任务，从一个点移动到另一个点，一般可以采用插值的方法，在起点和终点之间插入一系列点，由于约束的存在，就必须时时刻刻监视约束是否满足，这是非常困难的

Three Angle Representations

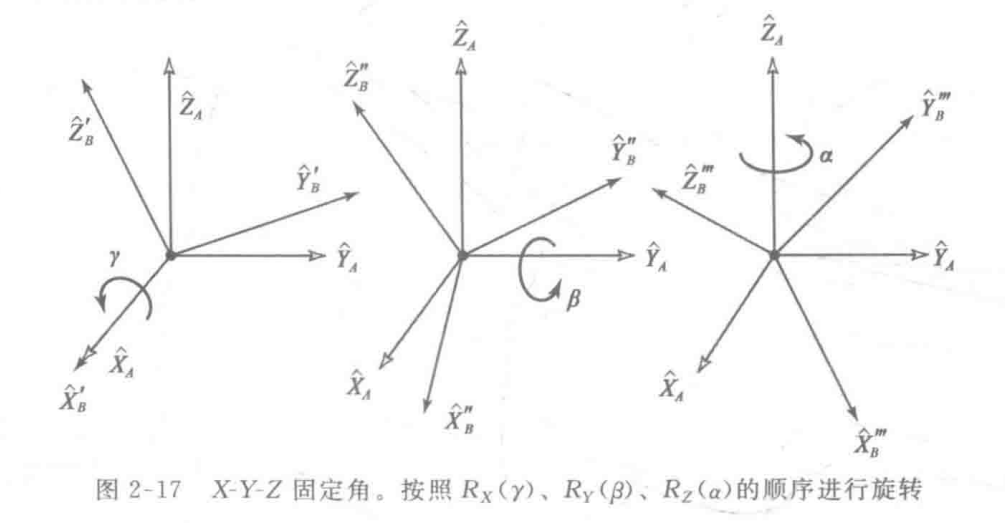
• Fixed Angles 固定角，即绕固定（参考坐标系）轴转

首先将坐标系{B}和一个已知的参考坐标系{A}重合。先将{B}绕旋转γ角，再绕旋转β角，最后绕旋转α角。由于每个旋转都是绕着固定参考坐标系{A}的轴，故称这种姿态表示法为X-Y-Z固定角。有时把它们定义为回转角、俯仰角和偏转角（roll、pitch、yaw）

可直接推导等价旋转矩阵：

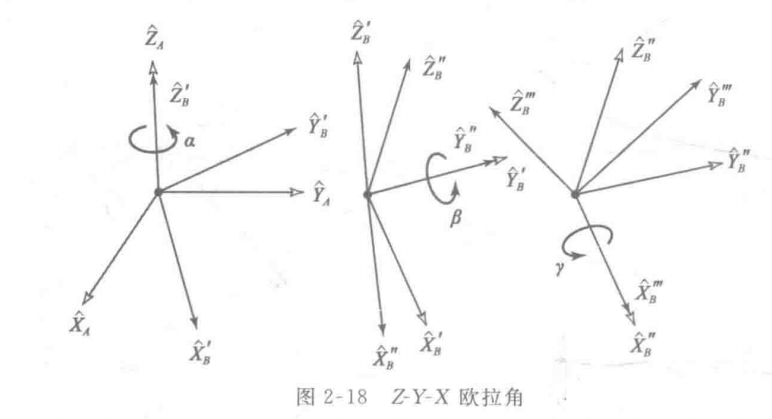
• Euler Angles (Z-Y-X)：Z-Y-X 欧拉角

首先将坐标系{B}和一个已知的参考坐标系{A}重合。先将{B}绕转α角，再绕绕β角，最后绕转γ角。在这种表示法中，每次都是绕运动坐标系{B}的各轴旋转而不是绕固定坐标系{A}的各轴旋转。这样三个一组的旋转被称作欧拉角。 注意每次旋转所绕的轴的姿态取决于上一次的旋转。

假设从坐标系A到B’，B’到B’’，B‘’到B的旋转矩阵分别是，显然

也可以写成

注意这个结果与以相反顺序绕固定轴旋转三次得到的结果完全相同。即三次绕固定轴旋转的最终姿态和以相反顺序绕运动坐标轴转动的最终姿态相同。

其中X是一些复杂的式子，但我们不关心，因此可以忽略。

至此得到了一个以转角α、β、γ为参数的旋转矩阵

• Z-Y-Z Euler Angles

懒得写了，还有很多不同转角组合，一共有24中表示法，称作转角排列设定法，其中12种为固定角设定法，另12种为欧拉角设定法。

Example

Inverse Problem

逆问题即从旋转矩阵等价推出X-Y-Z固定角

通过三角函数关系可以算出：

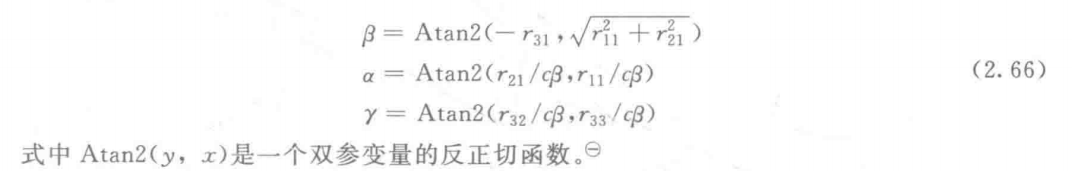
如果cosβ=0（β=±90°），以上的求解就不能成立，这样的点成为奇点（Singularity of the representation）。在这种情况下，只能求出α和γ的和或差，无法区分α和γ。在这种情况下一般取α=0

Example：

在奇点处将无法计算与α相关的速度，无法跟踪其运动 任何三参数的角度表示法都会遇到奇点问题，而方向余弦这种9参数的表示法没有奇点问题，但是有冗余

Equivalent angle-axis representation 等效角度-轴线表示

可以证明，总是存在一个向量，能够使坐标系A绕着向量旋转一定角度到坐标系B

首先将坐标系{B}和一个已知的参考坐标系{A}重合。将{B}绕矢量按右手定则转θ角。

是一个长度为1的单位向量，因此确定它只需要两个参数，角度确定了第三个参数。

经常用旋转量θ乘以单位方向矢量形成一个简单的3x1矢量来描述姿态，即

当选择{A}的主轴的其中一个作为旋转轴时，则等效旋转矩阵就变成了之前的平面旋转矩阵

若旋转轴为一般轴，则等效旋转矩阵为

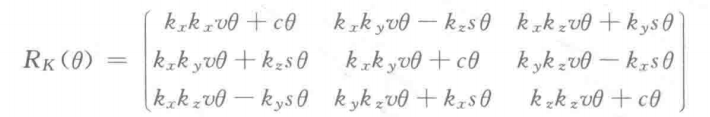
其中vθ=1-cosθ

从一个给定的旋转矩阵求和θ，这里直接给出结果，计算过程见书

由于这里sinθ在分母上，还是会有奇点问题

Euler Parameters 欧拉参数

欧拉参数通过4个数值表示姿态

给定旋转矩阵，得到对应的欧拉参数

• 引理：对于所有旋转，总是有一个欧拉参数大于或等于二分之一

虽然这里在分母上，但是欧拉参数表示法没有奇点问题

对于所有的，其值在[-1, 1]区间