Introduction to Robotics-Stanford 笔记 LEC2
这自动识别的字幕和机翻看得是真的费劲啊。。。
Spatial Descriptions 空间描述
- Task Description: 确定机器人的位置、框架、连杆和关节
- Transformations: 知道一个连杆/构件（这里把一个机械臂描述成连杆和关节组成的链条）的位置时，将该描述转换成下一个link的描述或者前一个link的末端位置和方向
- Representations: 如何表示位置和方向
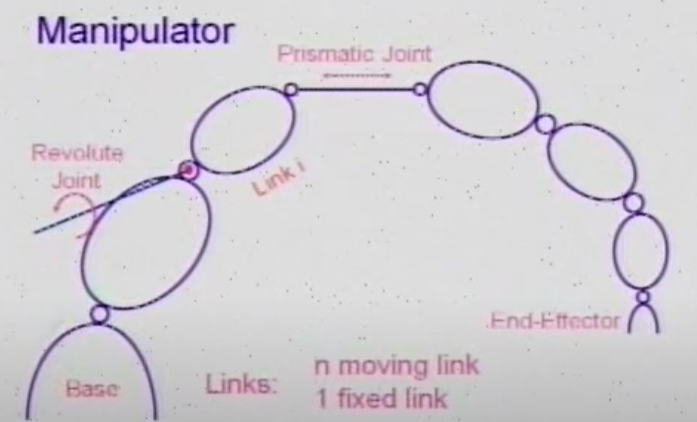
任何一组关节都可以简化为两种类型的关节：旋转关节（Revolute joints）和棱柱关节（Prismatic joints）。旋转关节允许围绕固定轴旋转，棱柱关节允许沿着固定轴平移假设有
n个移动link和1个固定link
Configure Parameters
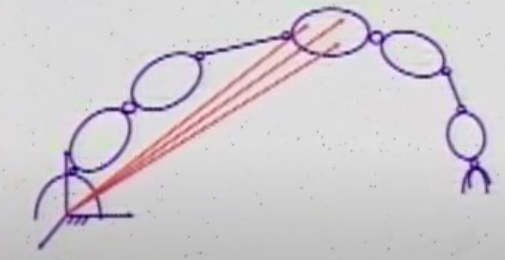
- 定义：A set of position parameters that describes the full configuration of the system.
- 问题描述：我们如何表示manipulator的配置，因为我们需要知道manipulator在空间中相对于固定框架的位置
- 一种方法是在link的三个不同点使用三个向量（？），由此定义一个link。在这种情况下，每个向量在三维空间中有三个参数，因此描述一个link需要9个参数，则一共需要9n个参数，参数量很大。实际上不需要三个点三个向量中的所有参数，因为这三个向量实际上不是相互独立的
- 需要找出一组具有最小数量的特定参数集配置参数：Generalized coordinates
- Generalized coordinates: A set of independent configuration parameters
- 本质上是一组配置参数，带来完全独立的参数，通过它们可以发现动力学，可以直接提供机器人的自由度数
Generalized Coordinates
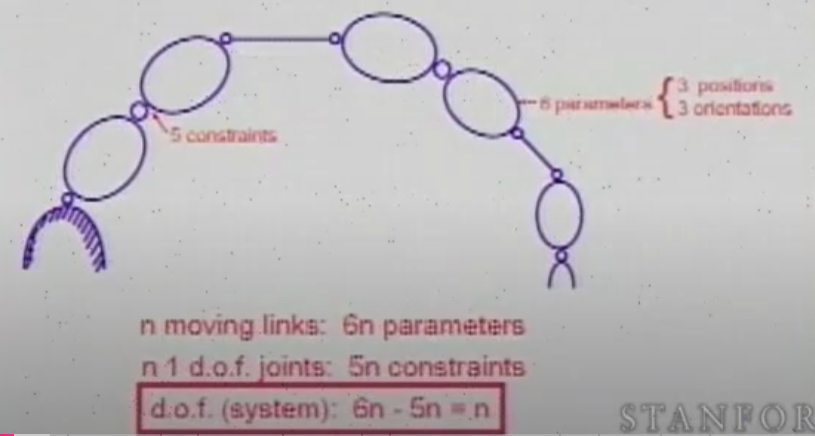
- 自由度讨论：假设断开关节只考虑每个link，视作一个自由刚体，一个刚体有6个自由度，一共6n个自由度；单独考虑关节，由于旋转关节和棱柱关节都只有一个自由度，引入了5个约束，因此总共有5n个约束。因此总自由度是6n-5n=n
End-Effector Configuration Parameters 末端执行器配置参数
- A set of m parameters:
that completely specifies the end-effector position and orientation with respect to {0} (fixed frame) 注意这里的m个参数并不一定是独立的 - 例如旋转矩阵（方向余弦矩阵）等
- 例如旋转矩阵，其中共有9个参数，如果再加上三个表示平移的参数，一共12个参数就能表示末端执行器的位置和方向。
Operational Coordinates
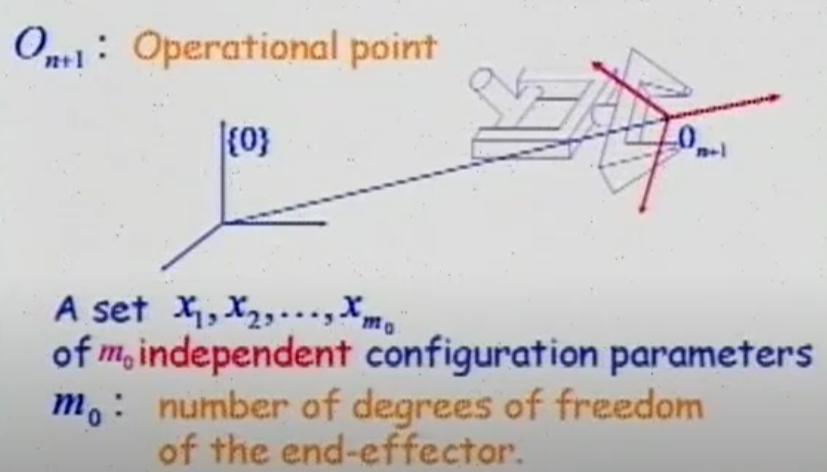
- Operational Point：机器人在我们定义任务的地方起作用的点
- 例如夹取任务，Operatinal Coordinates可能是两个夹爪之间的某个点
- Operational Coordinates: A set of m0 independent configuration parameters.
- m0: number of degrees of freedom of the end-effector，m0是等于末端执行器自由度数
- 注意这里的m0个参数是独立的
Joint Coordinates
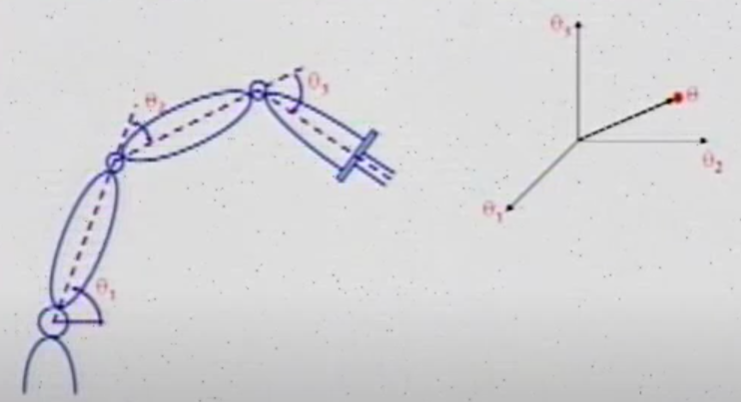如图中的一个平面机器人，拥有三个旋转关节
关节空间在运动规划中起着非常重要的作用
Operational Coordinates
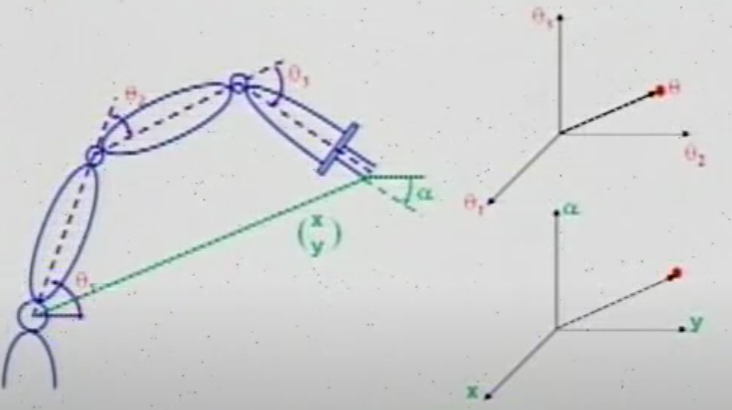对于末端执行器来说，可以用向量
由此，一个机器人被简化成了关节空间里的一个点
，末端执行器被简化成了操作空间的一个点 。这两个空间完全描述了机器人的配置。
新的问题：如果给机器人添加一个关节，那么配置可能会有所不同，即存在冗余
Redundancy 冗余
A robot is said to be redundant if :
如果机器人的自由度n大于末端执行器的自由度，则称其为冗余机器人。
冗余有很多作用，例如可以帮助机器人在各种配置下绕过障碍物。
- Degrees of redundancy冗余度：
Position of a Point
如何定义空间中的一个点？描述一个点的位置一定是相对于某一个点来讲的。
With respect to a fixed origin O, the position of a point P is described by the vector OP or simply by p.
Coordinate Frames 坐标系
旋转与平移的变换对刚体描述的影响，这里都是些坐标系变换的知识
Rotation Matrix 旋转矩阵
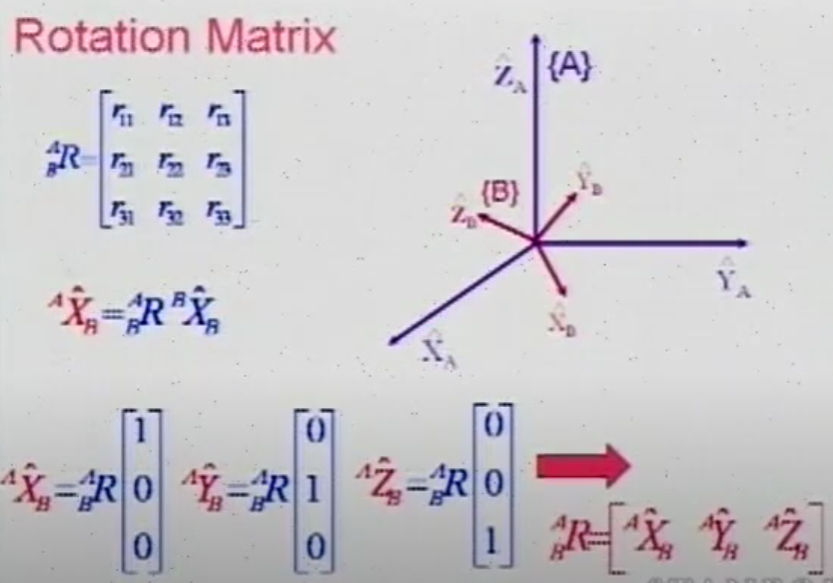
坐标系A到坐标系B的旋转矩阵就是
在坐标系A中的分量，即旋转矩阵的列是新坐标系的XYZ轴在原坐标系下的分量，通过点乘就可以得到：
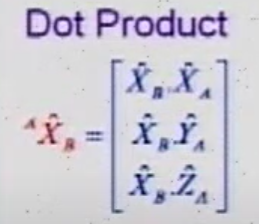
此外可以发现，旋转矩阵的行，是
在坐标系B中的分量的转置，即旋转矩阵的行是原坐标系的XYZ轴在新坐标系下的分量
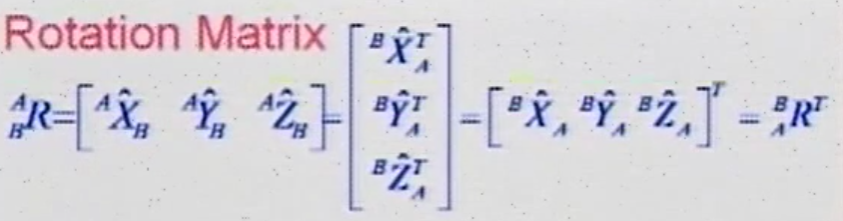
一个结论：A到B的旋转矩阵和B到A的旋转矩阵是转置关系，同时A到B的旋转矩阵和B到A的旋转矩阵是互逆的，所以有以下关系：
数学上的理解：由于坐标轴总是规范正交的，因此旋转矩阵的行向量/列向量之间也是规范正交的，正交矩阵的转置等于它的逆矩阵。 ### Example: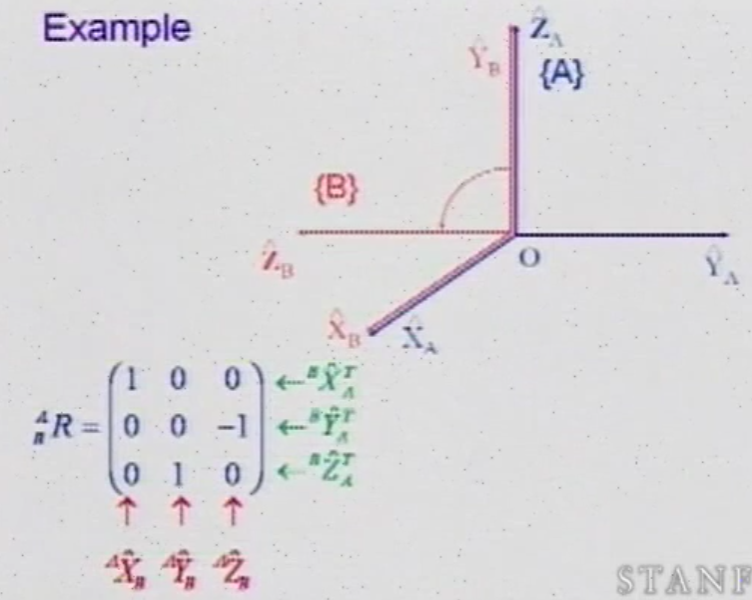 
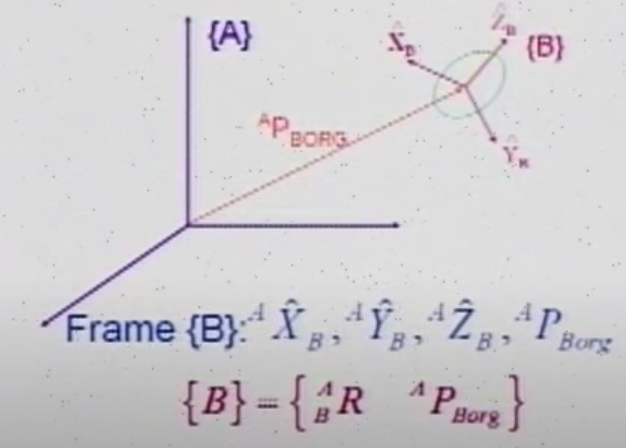
Description of a Frame with respect to reference fame
通过旋转矩阵和B相对于A原点位置向量：
Mapping
changing vector descriptions from frame to frame
Rotations
Translations
changing the position description of a point P
General Transform
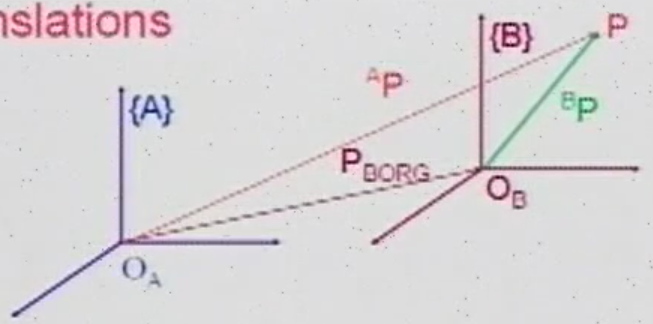
在连杆之间应用一般变换，我们应该能够计算并传播构件，但这个描述并不容易实现，因为当有很多个构件时，矩阵乘法和矩阵加法混在一起
处理这种转换的更好方法是尝试将其以齐次形式呈现 这是在三维空间的两个向量的和，不能以齐次形式表示，但如果进入四维空间，就可以将其以齐次形式表示，只需要多加一行：
Example：
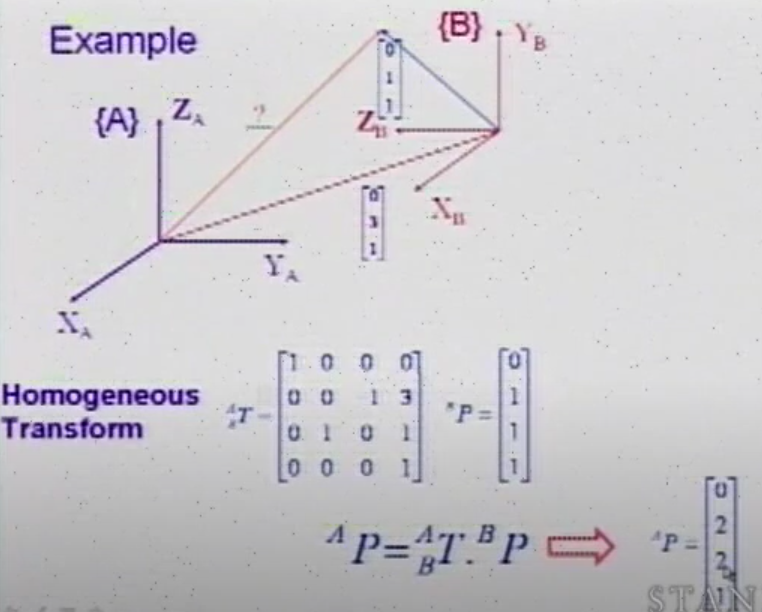
Operators
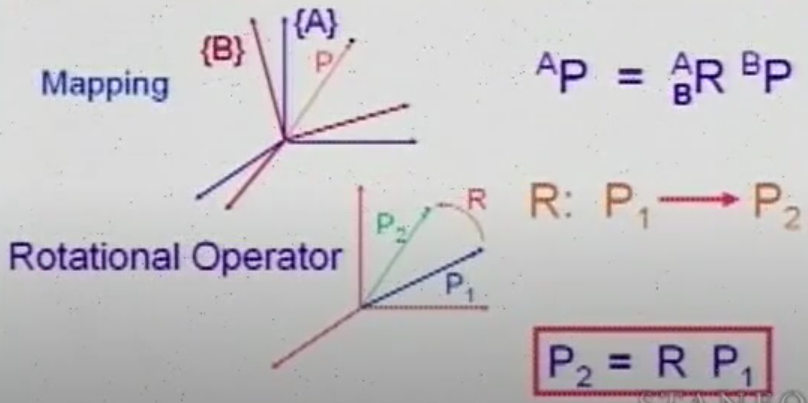
- Mapping: changing descriptions from frame to frame
- Operators: moving points (within the same frame)
映射并没有改变点，只是将点在一个坐标系下的表述转换成了另一个坐标系下的描述； 操作改变了点，并且仍然在原坐标系下描述。
Rotational Operators
Translations
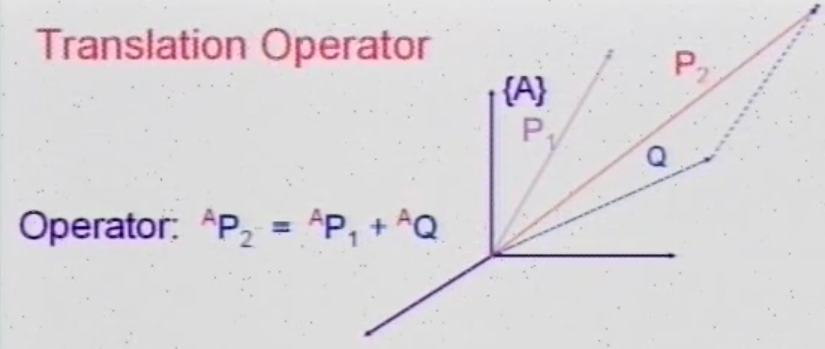
注意，应用平移操作时，必须确保Q和P1在同一坐标系下进行描述，并且结果也是在同一坐标系下的描述
General Operators
必须确保对所有操作使用相同的坐标系
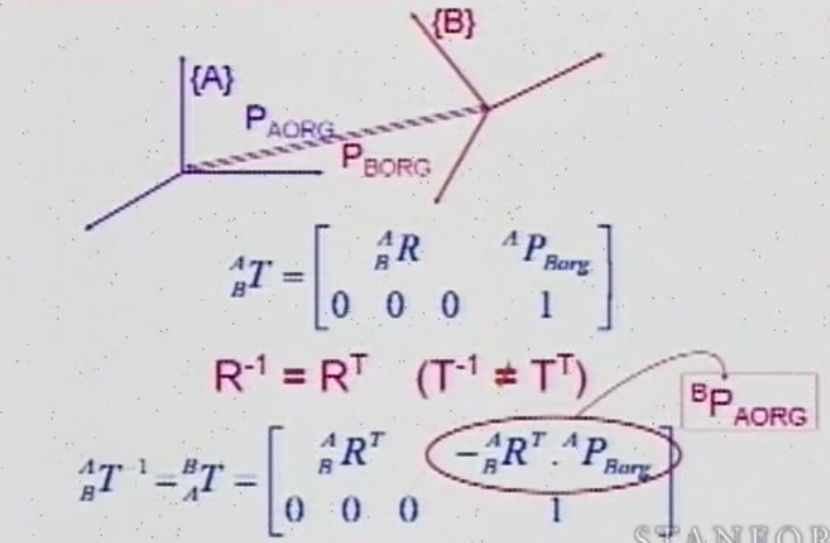
Inverse Transform
由于引入平移向量变成齐次形式，广义变换矩阵并不一定是正交的，也就不能像旋转矩阵一样直接求转置当成逆矩阵。 可以考虑分块矩阵：
